单光子源原理及实验测量分析

单光子产生原理^[1]:

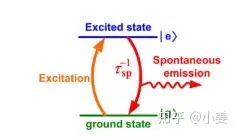
考虑理想的二能级系统（例如quantum dots量子点等），如图一，电子是费米子，根据泡利不相容原理，电子占据激发态而尚未产生自发辐射时，无法激发下一个电子到同一激发态^[1][2]。

也就是说无论外界怎么激发（连续激光或脉冲激光或是电致激发），该系统只能在自发辐射寿命期间（约ps到ns时间尺度）发射出一个光子，即不可能在某一时刻同时发射两个及以上数量的光子^[3]，即单光子源（术语：antibunching，反聚束），通俗的讲就是光子是一个接着一个发射，它们每次发射时间间隔和自发辐射寿命有关。

此外，”时刻“这个概念在实际操作过程中很值得玩味，毕竟人造的测试系统时间都是离散的，自然界时间是连续的，测试相当于一个采样过程。

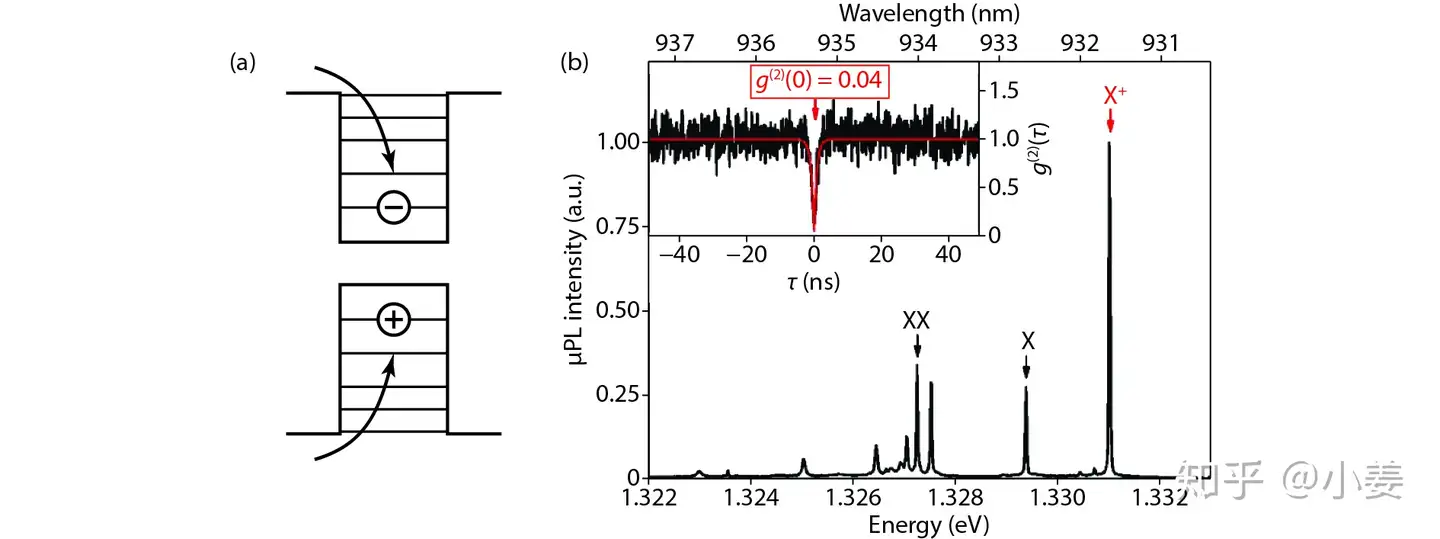
当然很难保证一个系统里面只有一个发光中心（emitter)^[4]，此时为聚束(bunching)，即某一时刻光源发出大量的光子，例如LED灯，热发光等这是自然界非常普遍的发光行为。史砚华教授提到的混沌热光的反聚束^[5]暂不讨论。

实验目的很简单:统计待测光源在某一时刻倾向于只发射一个光子还是一堆光子。

excited state：激发态；ground state：基态；spontaneous emission：自发辐射；excitation：外界激励源；
τsp−1 ：自发辐射寿命,单位秒 s ；
ps/ns皮秒，纳秒 ⇔ picosecond= 10−12s，nanosecond= 10−9s

测试实验装置：Hanbury Brown and Twiss experient^[6][7]

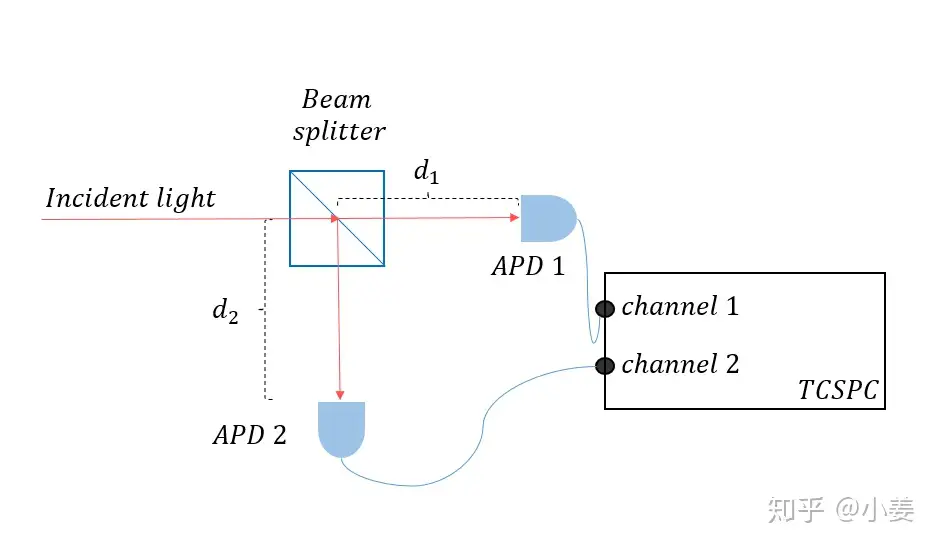
该装置包括三个部分:

• 50/50分束器，beam splitter，如图二：可以把一束的光强几乎等分成透射和反射两个部分^[8]。顺带说一下APD的后脉冲afterpulse（也叫breakdown fluorescence）
• 两个探测器，APD^[9](Avalanche Photodetector)，在盖格模式下（电源正负极千万不能接反），通过吸收一个光子产生一个电子空穴对来触发强雪崩^[10]，每探测到一个光子都能使APD发出一个上升沿信号，该信号被TCSPC接收以及记录。 为什么需要两个APD？答：因为每个APD都有固定的死时间（dead time）^[11]，探测完一个光子后需要20ns左右时间来排空电容电荷，以继续探测下一个光子，但是单光子的核心统计数据只发生在几个ns期间，如果只使用一个APD则会遗漏大量统计数据，如图三灰色圆圈代表在死时间内无法被探测到的光子，导致我们无法判定某光源是否为单光子源；但是如果用两个APD，通过50/50分束器-spliter，由于单个光子不可分割性，一定会进入其中一个APD，那么探测到间隔为ps时间尺度的两个光子事件可能性就有了，此时测试精度取决于APD固有的死时间还有correlator（时间相关仪）的死时间和时间分辨率。 另外,好一点的APD死时间大概20ns，接近四万人民币，死时间越小暗计数率越低仪器越贵，探测精度越高。当然如果有一天技术可以研发出dead time死时间在ps皮秒量级的APD，那完全可以只用一个就足够判定单光子源。

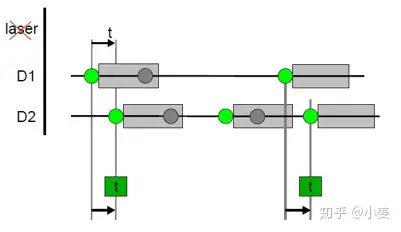
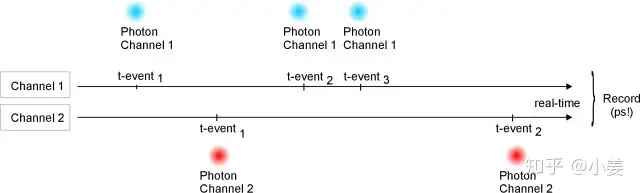
• TCSPC，时间相关仪(Time-Correlated Single Photon Counting)。如图四，此为典型双通道的TCSPC，通道 1,通道 2独立接收两个APD 1/APD 2传来的上升沿信号，以记录光子到达APD的绝对时间（也叫记录光子事件）。TCSPC每个通道内也有接收上升沿信号的死时间，我们用的国产的TCSPC死时间小于10ns^[12]；

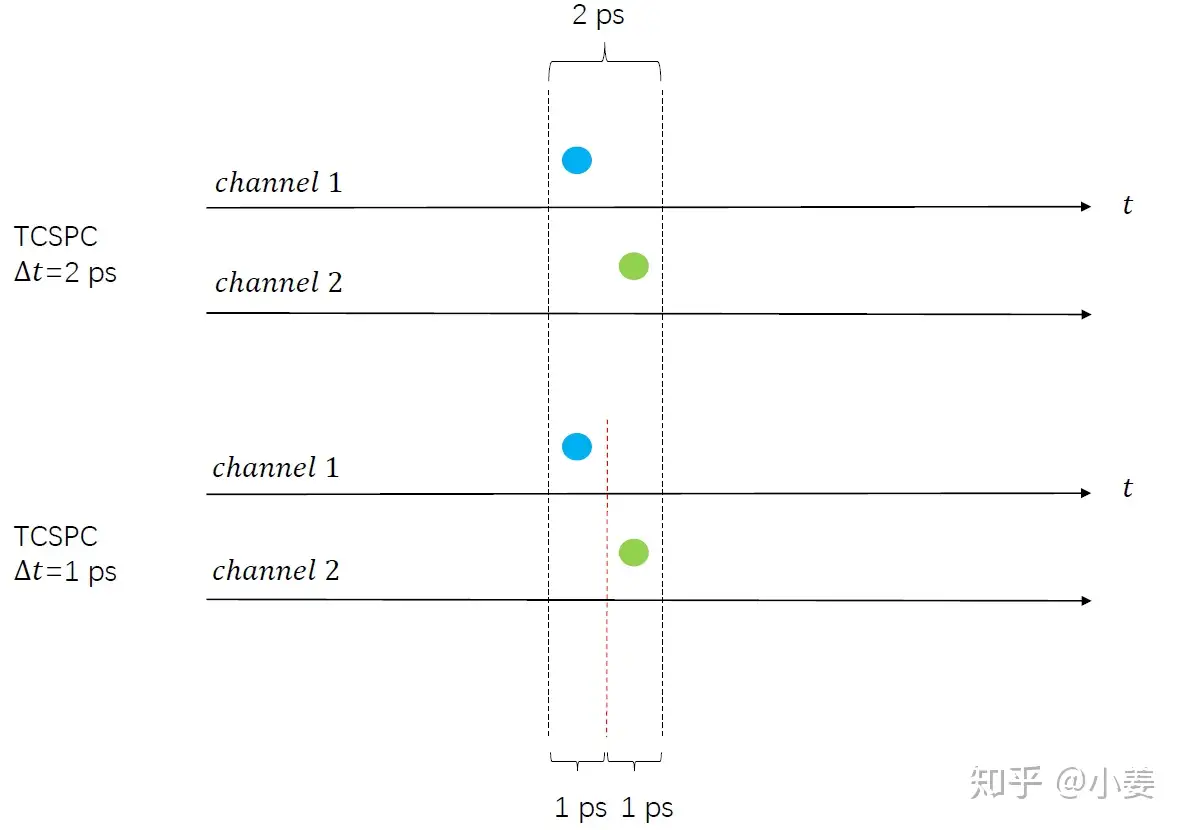
另外TCSPC还有时间分辨率，理想情况下采集时间是连续的，现实情况是仪器的采集时间都是离散的^[13]（可以看作数学上实数和有理数的区别），即存在一个最小采集时间间隔 ΔtTCSPC ，称之为时间分辨率。时间分辨率越高意味着测试系统越能分辨光子到达APD的先后顺序或者同时性，这对判定发光源同一时刻是否有两个光子发射有极其重要的影响！目前使用的是 ΔtTCSPC=64ps ，市场上^[14]也有 ΔtTCSPC=1ps 左右的分辨率，很贵。

单光子源判定公式( correlation function；符合计数 K /coincidence counts)^[15][16]：

g2(τ)=<I1(t)⋅I2(t+τ)><I1(t)><I2(t+τ)>
=limT→∞1T∫0TI1(t)⋅I2(t+τ)dtlimT→∞1T∫0TI1(t)dt⋅limT→∞1T∫0TI2(t+τ)dt

• τ 是延迟时间变量( time-lag variables^[17]），理想情况下是连续变量，但在实际测试中是离散变量，因为仪器记录的光子到达时间是离散的，这和时间相关仪时间分辨率 ΔtTCSPC 有关。
• <I(t)> 指光强的数学期望值， <I(t)>=<∑iEi∗(t)∑jEj(t)> ,其中需要考虑子场所有可能的复振幅的值^[5](Maxwell经典光学角度）。
• 需要指出 <I1(t)>=<I1(t+τ)> ， <I2(t)>=<I2(t+τ)> 具体推导暂不讨论；

实验核心操作：将APD的光子计数转化为 g2(τ)

因为 I1(t)∝n1(t),I2(t)∝n2(t) ;

，n1(t)，n2(t) 代表APD1/APD2测到的 t 时刻光子数 ⟹

g2(τ)=<n1(t)⋅n2(t+τ)><n1(t)><n2(t)>
分子是关键也叫符合计数 K ，分母是用来归一化；

• 时间相关仪(TCSPC)时间分辨率 ΔtTCSPC=64ps，测试总时间记为 T
• 通道1 (channel 1)接收总光子数为 N1 ，通道2（channel 2)接收总光子数为 N2
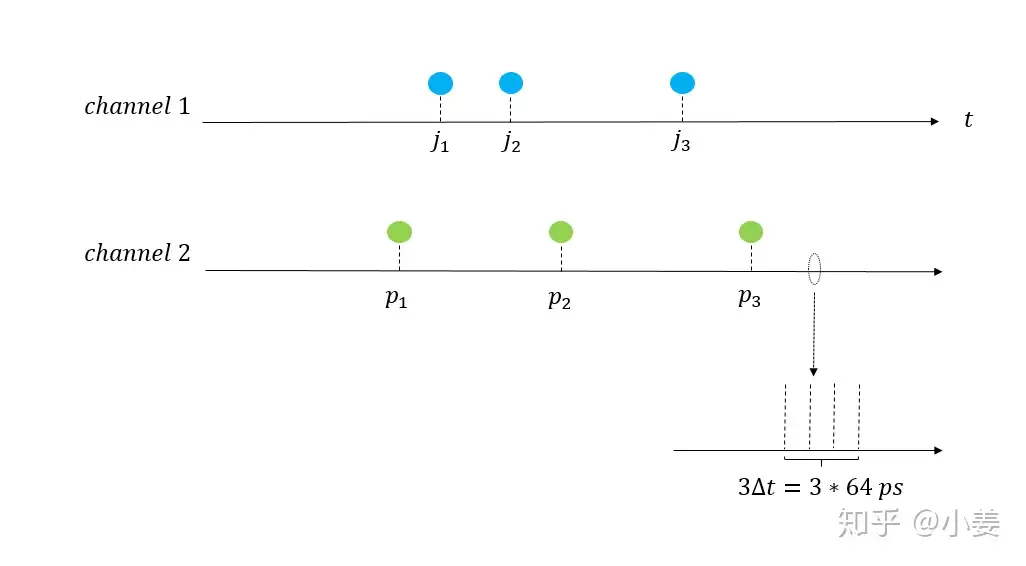
• 如图五，记 jm 为第 m 个光子到达 APD 1 的绝对时间， pn 为第 n 个光子到达APD 2 的绝对时间； m∈(0,N1]∩Z+ ; n∈(0,N2]∩Z+
• τ 指到达两个APD任意光子对 ∀(jm,pn) 绝对时间的差值^[17]，单位是时间

τ=jm−pn=X⋅ΔtTCSPC (X∈Z=...−2,−1,0,1,2...) ,最笨的算法要计算 N1×N2 个 τ 值，其中很多都是相同的 τ 值，把相同的 τ 值个数对应的排列起来都会得到相关函数-correlation function的分子，即符合计数 K 。


定义符合计数 K ：例如Kτ=0={(jm,pn)∣(τ=jm−pn=0⋅ΔtTCSPC=0)} ， Kτ=0 指符合 τ=0 所有光子对 (jm,pn) 集合的元素个数，通俗讲就是任意光子对时间差值等于0的个数（中括号是集合的意思，公式看不懂翻一下高中数学的集合和集合元素的个数）。

本质就是把 T 时间内采集的N1×N2 个离散 τ 绘制成关于时间的直方图-histogram，纵坐标就是符合计数，如图六（定义x 轴最小变化量：Δxmin=ΔtTCSPC=64ps ）

图六形象点说就是把 N1×N2 个小球放入 TΔtTCSPC 个盒子中，然后观察小球分布情况，一个盒子放了很多小球或者盒子没有球都是可能的，经过大量的采集、计算之后，单光子源的背后物理规律即被挖掘出来,统计学的中心思想是通过观察小样本即可得到整个群体的信息。

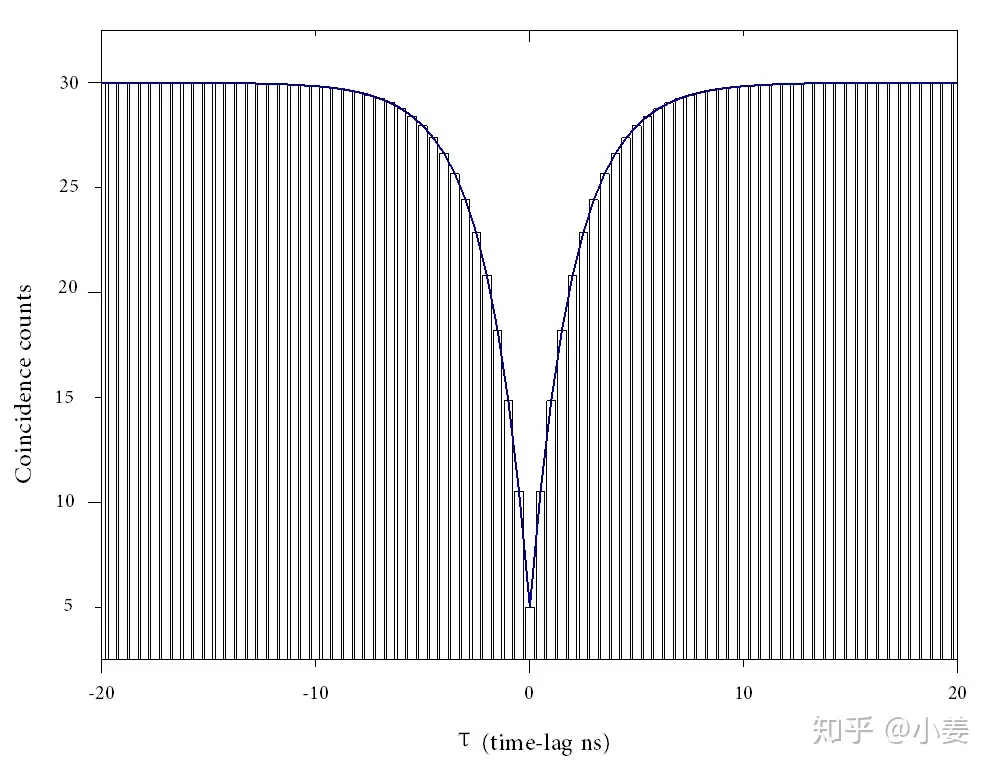
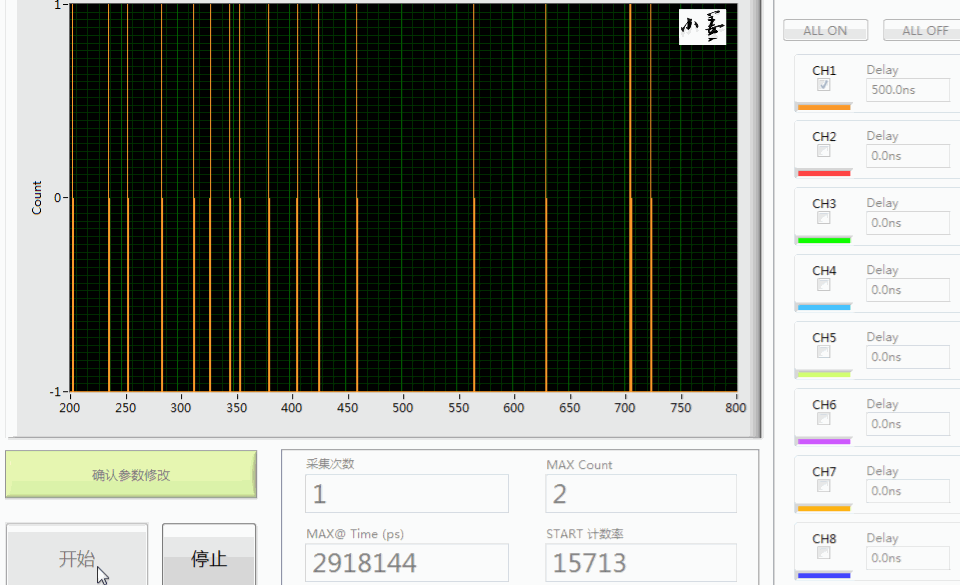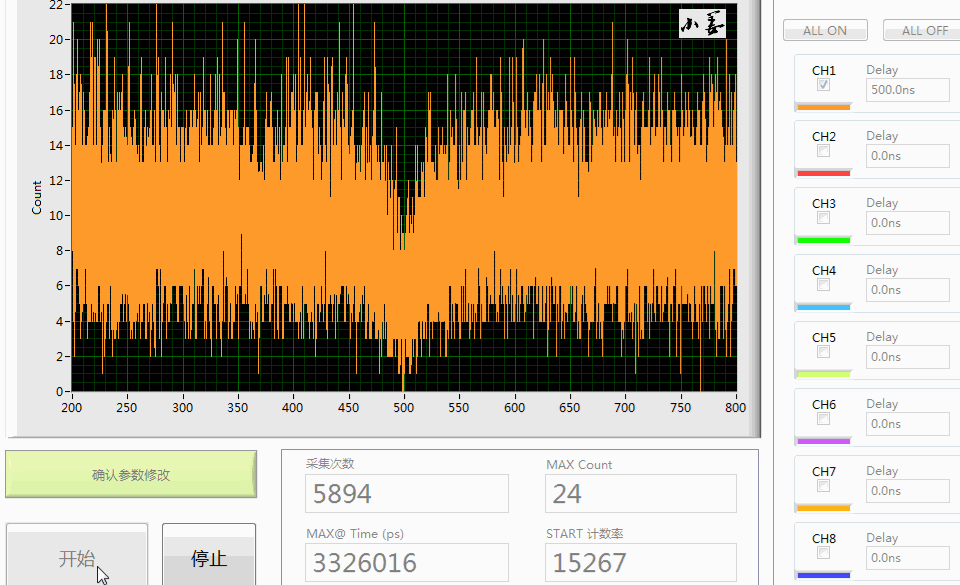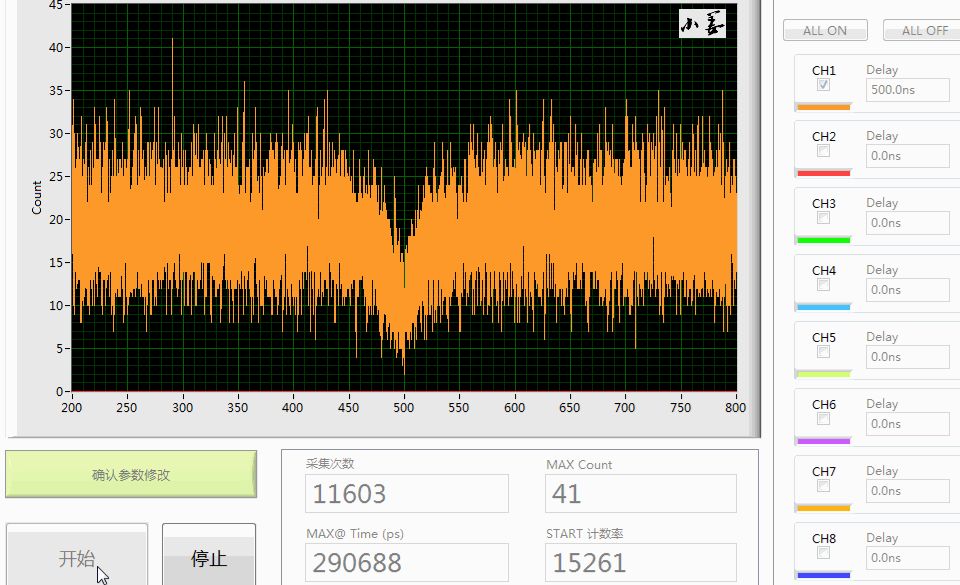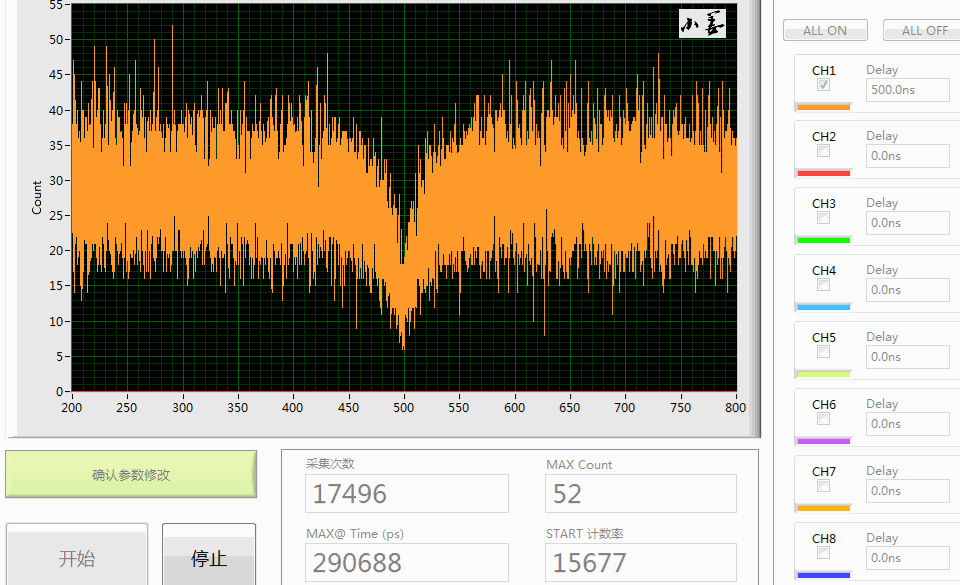
• 既然光子有先后到达（差值即有正有负），所以数据看起来关于 τ=0 对称，例如

τ1,1=j1−p1<0,τ1,2=j1−p2>0

• 理想情况下为什么 g2(τ=0)=0 ？？

既然是单光子源，光子在自发辐射寿命内只发射一个光子，整体表现为光子是一个接着一个发射，那么符合计数 Kτ=0={(jm,pn)∣(τ=jm−pn=0)}=∅，空集元素个数为0 。那么问题来了，符合计数是二阶相关函数的分子，分子都为0，零除以任何归一化常数结果都为零。

禁硕博论文抄袭！

附录（appendix）

• TCSPC时间分辨率 Δt 的意义及重要性：到底两个光子是不是”同一时刻“到达？不同时间分辨率的TCSPC给出的答案不一样！

参考

1. ^^abSenellart P, Solomon G, White A. High-performance semiconductor quantum-dot single-photon sources[J]. Nature nanotechnology, 2017, 12(11): 1026. https://www.nature.com/articles/nnano.2017.218.pdf
2. ^半導體量子光學-張文豪 徐子民 http://www.doc88.com/p-9911678777472.html
3. ^Wang H, He Y M, Chung T H, et al. Towards optimal single-photon sources from polarized microcavities[J]. Nature Photonics, 2019: 1-6.
4. ^Non-Poissonian photon statistics from macroscopic photon cutting materials-de Jong, Mathijs Meijerink, Andries Rabouw, Freddy T. https://www.nature.com/articles/ncomms15537
5. ^^ab史砚华. 量子光学导论：单光子和双光子物理[M]. 高等教育出版社, 2016.
6. ^The Quantum Theory of Optical Coherence-Glauber, Roy J.-Physical Review-1963 https://link.aps.org/doi/10.1103/PhysRev.130.2529
7. ^Hanbury Brown, R. and Twiss, R.Q., "A Test of a New Type of Stellar Interferometer on Sirius". Nature 178, 1046– 1048 (1956).
8. ^平板分束器 https://www.thorlabschina.cn/newgrouppage9.cfm?objectgroup_id=5111&pn=BSW26#11507
9. ^SPCM-AQRH https://www.excelitas.com/product/spcm-aqrh
10. ^教程：盖格模式 https://www.thorlabs.com/newgrouppage9.cfm?objectgroup_id=5255
11. ^Koberling F, Kraemer B, Buschmann V, et al. Recent advances in photon coincidence measurements for photon antibunching and full correlation analysis[C]//Single Molecule Spectroscopy and Imaging II. International Society for Optics and Photonics, 2009, 7185: 71850Q.- F. Koberling B. Kraemer V. Buschmann S. Ruettinger P. Kapusta M. Patting M. Wahl R. Erdmann
12. ^http://www.siminics.com/Goods/Detail?id=1
13. ^Laurence T A, Fore S, Huser T. Fast, flexible algorithm for calculating photon correlations[J]. Optics letters, 2006, 31(6): 829-831.
14. ^PicoHarp 300 https://www.picoquant.com/products/category/tcspc-and-time-tagging-modules/picoharp-300-stand-alone-tcspc-module-with-usb-interface#custom2
15. ^Boitier, Fabien, et al. "Measuring photon bunching at ultrashort timescale by two-photon absorption in semiconductors." Nature Physics 5.4 (2009): 267.
16. ^Walls D F, Milburn G J. Quantum optics[M]. Springer Science & Business Media, 2007.
17. ^^abLaurence T A, Fore S, Huser T. Fast, flexible algorithm for calculating photon correlations[J]. Optics letters, 2006, 31(6): 829-831.

本文引用自：单光子源原理及实验测量分析 - 知乎 (zhihu.com)